Blog scientifique, technologique, environnemental et politique de Nicolas HAHN

Comment est-ce donc possible?

Par exemple, on utilise les nanotechnologies dans le cadre d'opérations de dépollution. Des expériences sont faites pour dépolluer l'eau de composants comme l'arsenic, les métaux lourds, etc. La méthode traditionnelle, c'est de faire passer l'eau à dépolluer au travers de membranes, c'est à dire au travers d'une surface de filtration micro-poreuse qui laisse passer les molécules d'eau, et pas les molécules des composés polluants. Pour une dépollution efficace un minimum, il faut donc une grande surface de filtrage.

Si maintenant on dépollue l'eau par utilisation de matériaux de taille nanométrique (nano = 10 puissance -9) agissant comme des capteurs des composés polluants, alors on a besoin d'appareils beaucoup moins volumineux pour faire un travail plus efficace, puisque là, il faut plutôt penser en volume au lieu de surface. Autrement dit dans un volume donné, on a une certaine quantité de matériel à l'échelle nanométrique; pour imager, on a une certaine quantité de billes ayant une taille de l'ordre du nanomètre. La surface de ces billes, collectivement, représente la surface de filtrage.

Pour clarifier, on va faire un peu de mathématiques. Oui je sais, moi non plus j'aime pas les maths...

Quelle est la surface d'un terrain de foot?

Posons les données de façon correcte, car pour commencer, il y a plusieurs dimensions. On va donc prendre celles applicables pour les matchs internationaux, précisées par la loi 1 du football établie par l'IFAB. Cette loi précise les dimensions suivantes:

• longueur: entre 100 et 110 mètres
• largeur: entre 64 et 75 mètres

Je vais donc utiliser ici une surface de 110 mètres par 75 mètres, à savoir 8250 m2 (mètres au carré).

C'est grand, hein...

Maintenant, l'exercice va consister à savoir si une si grande surface pourrait être contenue dans un volume qui permettrait un transport par "être humain", c'est à dire un objet, un "contenant", qui contiendrait une certaine quantité de billes de taille nanométrique qui soit empoignable avec les deux mains d'une personne.

On a donc la surface du terrain de foot. Pour nos billes nanométriques, il nous faut la formule permettant de calculer la surface, l'aire, d'une sphère:

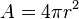
Maintenant, disons que notre sphère est rangée dans une boite, c'est à dire un cube, de 10 centimètres de côté, et que la sphère rentre pile dans la boite, c'est à dire qu'en tout côté du cube, la sphère est en contact. Cela revient à dire que la sphère à un diamètre de 10 centimètres, ou si vous préférez un rayon de 5 centimètres.

La surface de notre unique sphère dans sa boite est donc, selon la formule exposée ci-dessus, de 314,15926535897932384626433832795 cm2 (centimètres au carré).

A titre de comparaison, si l'on calculait la surface du cube, c'est à dire la surface de tous ses côtés, on arrive à un cumul de 6 x (10 au carré) = 600 cm2.

L'esprit vif qu'est le vôtre aura tout de suite remarqué que la surface de notre sphère, est inférieure à la surface de tous les côtés du cube.

Ensuite, disons que dans la même boite, on souhaite transporter plus de billes, des billes deux fois plus petites en diamètre. Au lieu donc d'avoir des billes de 10 centimètres de diamètre, on va ranger des billes de 5 centimètres de diamètre dans notre cube de 10 centimètres de côté.

Combien de billes peut-on mettre dans notre cube? La réponse est 8: 2 étages de 4 billes dans le volume du cube.

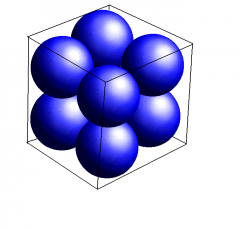
Ce qui est amusant maintenant, c'est de calculer pour commencer la surface d'une de nos sphères de plus petite taille que précédemment. On obtient 78,539816339744830961566084581988 cm2. Pour une seule de nos 8 billes!

Et donc pour obtenir la surface globale offerte par toutes nos sphères, on multiplie ce nombre par 8. On obtient donc une surface totale de 628,3185307179586476925286766559 cm2! Cette fois-ci la surface cumulée de toutes nos billes dans la boite dépasse la surface de tous les côtés de la boite. On utilise donc mieux l'espace de rangement de la boite, ou devrais-je plutôt écrire, le volume de rangement disponible dans la boite! On est donc plus efficace!

Autrement dit:

• à partir de maintenant je vais vous épargner la suite de chiffres après la virgule
• dans la même boite, en y rangeant des billes deux fois plus petites en diamètre, on en a mis 8 au total
• 8 billes de diamètre deux fois inférieur offrent une surface cumulée deux fois plus importante

Ce n'est pas de la magie, c'est juste des mathématiques.

Ensuite, vous avez compris le principe, on s'amuse de nouveau à mettre des sphères de diamètre encore deux fois plus petit dans notre boite de rangement, qui elle ne varie pas. Refaisons notre calcul pour des sphères de 2.5 centimètres de diamètre, soit 1.25 centimètre de rayon.

• On en met un total de 64 dans la boite.
• La surface d'une seule sphère de 1.25 cm de rayon est de environ 19.635 cm2.
• La surface cumulée de toutes nos sphères est de 64 x 19.635 cm2 soit 1256.637 cm2.

Conclusions: à chaque nouvelle itération vers l'infiniment plus petit...

• on multiplie le nombre de sphère par 8, c'est à dire 2 à la puissance 3. De 1 sphère, on est passé à 8. De 8, à 64. De 64, on passera à 512...
• on divise le rayon des sphères par 2
• on multiplie la surface totale par 2, ou encore la surface est égale à la surface de la toute première itération multipliée par 2 à la puissance du nombre d'itérations moins un. Par exemple, pour la troisième itération, cela donne 314.159 x 2 puissance (3-1) = 1256.637 cm2.
  

Tout cela en restant exactement dans le même contenant (dans la même boite de rangement dont les dimensions n'ont pas varié d'un iota).

Là, je vous ferais remarquer que nous en sommes seulement à la troisième itération. Et cette troisième itération nous donne une surface de 1256.637 cm2, soit 0.1256637 m2 (mètre au carré). On est encore très très très loin d'avoir atteint des sphères de diamètre nanométrique... On s'approche petit à petit de la surface de notre terrain de foot.

Quatrième itération:

• On met un total de 512 billes dans la boite
• La surface d'une seule sphère de 0.625 cm de rayon est de environ 4.91 cm2
• La surface cumulée de toutes nos sphères est de 2513.274 cm2, soit 0.2513274 m2.

5ème itération: 4096 sphères de 0.3125 cm de rayon, surface cumulée: 0.5026548 m2

On dépasse le mètre carré de surface à peine à la 6ème itération. L'augmentation de la surface est exponentielle, rappelez-vous, à chaque itération.

6ème itération: 1,0053096 m2
7ème itération: 2,0106193 m2
8ème itération: 4,0212386 m2
9ème itération: 8,0424772 m2
10ème itération: 16,0849544 m2
11ème itération: 32,1699088 m2
12ème itération: 64,3398175 m2
13ème itération: 128,6796351 m2
14ème itération: 257,36 m2
15ème itération: 514,72 m2
16ème itération: 1029,44 m2
17ème itération: 2058,87 m2
18ème itération: 4117,75 m2

19ème itération: 8235,49 m2

Et voilà! Il aura fallu arriver à la 19ème itération pour que toutes les billes dans notre boite représentent une surface cumulée un petit peu plus petite mais néanmoins équivalente à la surface d'un terrain de football!

Notre boite de rangement - un cube de 10 centimètres de côté - contiendra alors:

• 18014398509481984 billes (c'est à dire environ 18014,3985 millions de millions de billes)
• qui ont un rayon de 0,000019073486328125 cm (c'est à dire 0,000191 millimètres, ou encore 0,1907 micromètres, ou encore 190.7348 nanomètres)

Nous y sommes! Quelques données pour finir:

• Notre terrain de foot de 8250 m2 tient dans un rubik's cube de 10 centimètres de côtés plein de billes de 190.7348 nanomètres de rayon
• Notre rubik's cube continue néanmoins d'être plein de vide (l'espace entre les billes). Il y a donc encore de la place pour le remplir! D'ailleurs, il y aura toujours de la place...
• Le diamètre d'un cheveux varie de 40 à 100 micromètres (information Wikipedia), c'est à dire entre 40000 et 100000 nanomètres. Si pour des raisons de facilité, on dit que nos billes ont un rayon de 200 nanomètres, donc un diamètre de 400 nanomètres, le cheveux est au minimum encore 100 fois plus gros que l'une de nos billes
• L'industrie sait fabriquer des matériaux d'une taille inférieure à 1 nanomètre, en réorganisant les atomes un par un. Nos billes sont donc encore énormes du point de vue des industriels qui peuvent en faire de beaucoup plus petites...
• la molécule d'ADN a une taille de l'ordre d'un nanomètre
• Les derniers processeurs Intel (Intel Core i7 par exemple) sont gravés en 22 nanomètres. Leur finesse de gravure est donc 17 fois plus petite que le diamètre de l'une de nos billes

Pour conclure, je dirais que

• dans le foot, les joueurs sont payés des millions d'euros par mois et ça sert à rien (oui j'aime pas, je déteste, j’exècre le foot...) et j'entends aujourd'hui que ces messieurs les joueurs se mettent en grève: c'est vraiment se foutre de la gueule du monde!!! Déjà que l'économie footballistique a tout d'une mafia... Que l'on ferme les stades et que l'on se débarrasse des joueurs, ou alors qu'on les enferme dans un rubik's cube: voilà ce que j'en dis! Mais ça fera sans doute l'objet d'un prochain article sur mon blog...
• les nanotechnologies sont d'une importance capitale pour le développement de la suite de mes articles sur mon blog, notamment et surtout au niveau des nouvelles technologies de stockage de l'énergie électrique qui reposent dessus
• les nanotechnologies sont d'une importance sans précédent tout court
• les nanotechnologies seront invisibles, absolument partout, et leur dangerosité pourrait être extrêmement importante si mal maitrisées

Vive le rubik's cube!

A bas le foot!